ฟังก์ชันตรีโกณมิติ
ซึ่งมีความสำคัญในการศึกษารูปสามเหลี่ยมและ
ปรากฏการณ์ในลักษณะเป็นคาบ ฟังก์ชันอาจนิยามด้วยอัตราส่วนของด้าน 2 ด้านของรูปสามเหลี่ยมมุมฉาก
ปรากฏการณ์ในลักษณะเป็นคาบ ฟังก์ชันอาจนิยามด้วยอัตราส่วนของด้าน 2 ด้านของรูปสามเหลี่ยมมุมฉาก
หรืออัตราส่วนของพิกัดของจุด
บนวงกลมหนึ่งหน่วย หรือนิยามในรูปทั่วไปเช่น อนุกรมอนันต์ หรือสมการเชิงอนุพันธ์
บนวงกลมหนึ่งหน่วย หรือนิยามในรูปทั่วไปเช่น อนุกรมอนันต์ หรือสมการเชิงอนุพันธ์
รูปสามเหลี่ยมที่นำมาใช้จะอยู่ในระนาบแบบยุคลิด
ดังนั้น ผลรวมของมุมทุกมุมจึงเท่ากับ 180° เสมอ
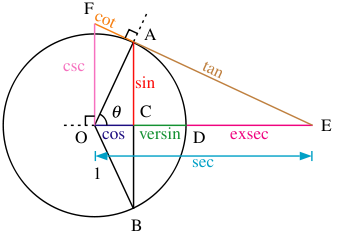
ในปัจจุบัน มีฟังก์ชันตรีโกณมิติอยู่ 6 ฟังก์ชันที่นิยมใช้กัน ดังนี้
วิธีการนี้ใช้จำค่าตรีโกณมิติของมุมพื้นฐานกล่าวคือ 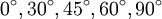
ลิงค์ดาวโหลดเอกสารฟรีได้ที่ ติวเตอร์ดีดี Library คลิก!
>>Download เอกสาร การเรียน ด้านคณิตศาสตร์ ฟรี
>>Download เอกสาร การเรียน ด้านวิทยาศาสตร์ ฟรี
ดังนั้น ผลรวมของมุมทุกมุมจึงเท่ากับ 180° เสมอ
ฟังก์ชันตรีโกณมิติพื้นฐานทั้งหมด
ในปัจจุบัน มีฟังก์ชันตรีโกณมิติอยู่ 6 ฟังก์ชันที่นิยมใช้กัน ดังนี้
| ฟังก์ชัน | ตัวย่อ | |
| ไซน์ (Sine) | sin | |
| โคไซน์ (Cosine) | cos | |
| แทนเจนต์ (Tangent) | tan (หรือ tg) | |
| โคแทนเจนต์ (Cotangent) | cot (หรือ ctg หรือ ctn) | |
| ซีแคนต์ (Secant) | sec | |
| โคซีแคนต์ (Cosecant) | csc (หรือ cosec) |
การใช้นิ้วมือช่วยในการจำค่าตรีโกณมิติของมุมพื้นฐาน
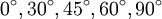
มีขั้นตอนดังต่อไปนี้
แบมือซ้ายออกมา มองเลขมุมจับคู่กับนิ้วเรียงจากซ้ายไปขวา
เป็นมุม 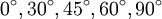 องศา
องศา
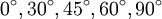 องศา
องศา
เมื่อต้องการหาค่าตรีโกณมิติของมุมใดให้งอนิ้วนั้น สมมติว่าหา cos 

ก็จะตรงกับนิ้วชี้ ก็งอนิ้วชี้เก็บไว้
ถือกฎว่า "sin-ซ้าย(ออกเสียงคล้ายกัน) cos-ขวา(ออกเสียง /k/ เหมือนกัน)"
เมื่อหาค่าของฟังก์ชันใดให้สนใจจำนวนนิ้วมือฝั่งที่สอดคล้องกับฟังก์ชันนั้น
เพื่อจะหาค่า นำจำนวนนิ้วมือด้านที่สนใจติดรากที่สองแล้วหารด้วยสอ
ง (หรืออาจจำว่ามีเลขสองตัวใหญ่ๆอยู่บนฝ่ามือ เมื่ออ่านก็จะเป็น
รากที่สองของจำนวนนิ้วมือด้านที่สนใจ หารฝ่ามือ)
สำหรับ cos 30 ก็จะได้ว่ามีนิ้วมือเหลืออยู่ทางด้านขวาอีกสามนิ้ว (กลาง นาง ก้อย)
ก็จะได้ cos30=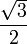 สำหรับฟังก์ชันตรีโกณมิติอื่นก็ใช้สมบัติของฟังก์ชันนั้นกับ
สำหรับฟังก์ชันตรีโกณมิติอื่นก็ใช้สมบัติของฟังก์ชันนั้นกับ
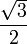 สำหรับฟังก์ชันตรีโกณมิติอื่นก็ใช้สมบัติของฟังก์ชันนั้นกับ
สำหรับฟังก์ชันตรีโกณมิติอื่นก็ใช้สมบัติของฟังก์ชันนั้นกับ
sin และ cos เช่น tan=sin/cos
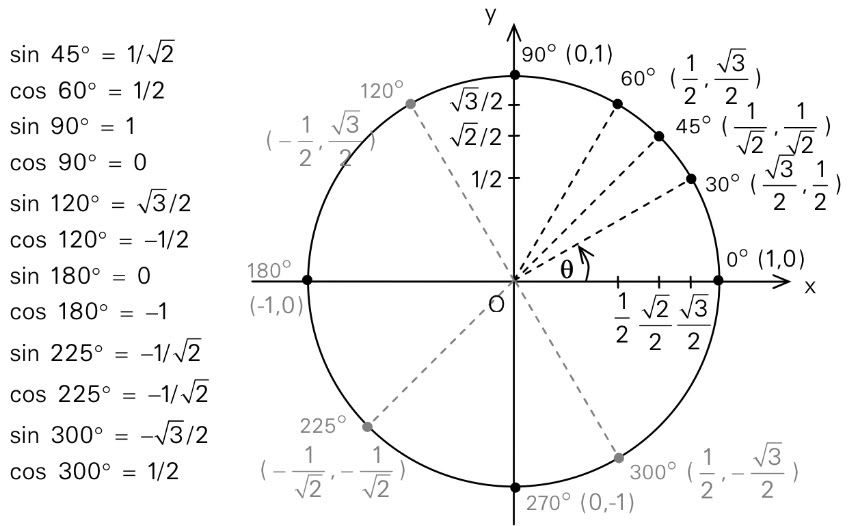
การกำหนดค่าของฟังก์ชันตรีโกณมิตินั้น สามารถทำได้โดยการใช้วงกลมรัศมี 1 หน่ว
ย มีจุดศูนย์กลางอยู่ที่จุดกำเนิด
และเราจะเรียกวงกลมดังกล่าวว่า วงกลมหนึ่งหน่วย (The unit circle)
- เมื่อเรากำหนดจำนวนจริง θ (ทีตา) จาก (1,0) วัดระยะไปตามส่วนโค้งของวงกลม โดยมีข้อตกลงดังนี้ว่า :
ถ้า θ > 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางทวนเข็มนาฬิกา
ถ้า θ < 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางตามเข็มนาฬิกา
ถ้า θ = 0 จุดปลายส่วนโค้งคือจุด (1,0)
จะได้ว่า เมื่อเรากำหนดจำนวนจริง θ ให้ เราสามรารถหาจุด (x,y) ซึ่งเป็นจุดปลายส่วนโค้งได้เพียงจุดเดียวเท่านั้น
ถ้า |θ| > 2π แสดงว่า วัดส่วนโค้งเกิน 1 รอบ เพราะเส้นรองวงของวงกลมยาว 2π หน่วย
เมื่อ (x,y) เป็นจุดปลายส่วนโค้งของวงกลมข้างต้น
y = sinθ (อ่านว่า วาย เท่ากับ ไซน์ทีตา)
x = cosθ (อ่านว่า เอกซ์ เท่ากับ คอสทีตา)
ฟังก์ชันไซน์และฟังก์ชันโคไซน์นั้น เป็นจำนวนจริง ตั้งแต่ -1 ถึง 1
นั่นคือ เรนจ์ของฟังก์ชันไซน์และโคไซน์ คือ เซตของจำนวนจริง ตั้งแต่ -1 ถึง 1
และโดเมนของฟังก์ชันทั้งสองคือเซตของจำนวนจริง
ค่าของฟังก์ชันไซน์และโคไซน์ เป็นดังตารางนี้
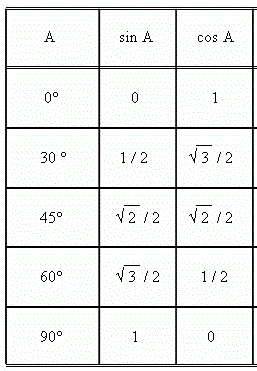
จากตาราง ทำให้เราสามารถสรุปได้ว่า
sin(-θ) = -sinθ
cos(-θ) = cosθ
มุมที่จุดศูนย์กลางของวงกลม ซึ่งรองรับด้วยส่วนของเส้นโค้งที่ยาว 2πr หน่วยจะมีขนาด 2π เรเดียน
และมุมที่จุดศูนย์กลางของวงกลม ซึ่งรองรับด้วยส่วนโค้งครึ่งวงกลมที่ยาว πr หน่วยจะมีขนาด π เรเดียน
จะเห็นได้ว่า สำหรับมุมที่จุดศูนย์กลางของวงกลมที่มีรัศมี r หน่วย ซึ่งรองรับด้วยส่วนโค้งของวงกลมมรายาว a หน่วย จะได้
และมุมที่จุดศูนย์กลางของวงกลม ซึ่งรองรับด้วยส่วนโค้งครึ่งวงกลมที่ยาว πr หน่วยจะมีขนาด π เรเดียน
จะเห็นได้ว่า สำหรับมุมที่จุดศูนย์กลางของวงกลมที่มีรัศมี r หน่วย ซึ่งรองรับด้วยส่วนโค้งของวงกลมมรายาว a หน่วย จะได้
θ = a/r
360 องศา เท่ากับ 2π เรเดียน
180 องศา เท่ากับ π เรเดียน
sin = ด้านตรงข้าม / ด้านตรงข้ามมุมฉาก
cos = ด้านประชิด / ด้านตรงข้ามมุมฉาก
tan = ด้านตรงข้าม / ด้านประชิด
cos = ด้านประชิด / ด้านตรงข้ามมุมฉาก
tan = ด้านตรงข้าม / ด้านประชิด
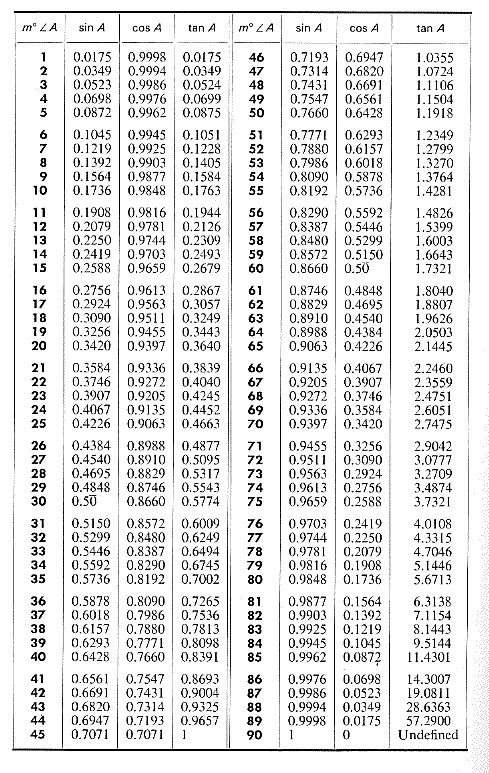
⑤ การใช้ตารางค่าฟังก์ชันตรีโกณมิติ
ทำการหาค่ามุมที่ต้องการทางด้านซ้ายมือของตาราง แล้ว นำมาเทียบกับค่าฟังก์ชันตรีโกณมิติทางด้านขวามือของตาราง เป็นอันเสร็จสิ้น
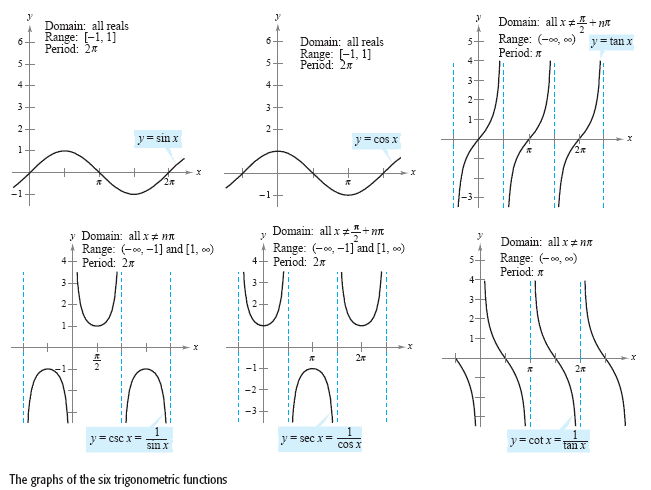
กราฟของฟังก์ชันตรีโกณมิติ
ฟังก์ชันตรีโกณมิติ ทุกฟังก์ชัน เป็นฟังก์ชันที่เป็นคาบ (Periodic Function)
กล่าวคือ สามารถแบ่งแกน x ออกเป็นช่วงย่อย (Subinterval) โดยที่ความยาวแต่ละช่วงย่อยเท่ากัน
และกราฟในแต่ละช่วงย่อยมีลักษณะเหมือนกัน ความยาวของช่วงย่อยที่สั้นที่สุดมีสมบัติดังกล่าวเรียกว่า คาบ (Period)
จากรูปข้างต้น จะเห็นได้ว่า
- คาบของกราฟ y = sinx และ y = cosx เท่ากับ 2π
- คาบของกราฟ y = cosecx และ y = secx เท่ากับ 2π
- คาบของกราฟ y = tanx และ y = cotx เท่ากับ π
สำหรับฟังก์ชันที่เป็นคาบซึ่งมีค่าสูงสุดและค่าต่ำสุด
เราจะเรียกว่าที่เท่ากับครึ่งหนึ่งของค่าสูงสุดลบด้วยค่าต่ำสุดของฟังก์ชันนี้ว่า แอมพลิจูด (Amplitude)
- ฟังก์ชัน y = sinx และ y = cosx มีแอมพลิจูดเป็น 1 เท่ากัน
ชมคลิป


ไม่มีความคิดเห็น:
แสดงความคิดเห็น